题目
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。
如果一个星星的左下方(包含正左和正下)有 颗星星,就说这颗星星是 级的。
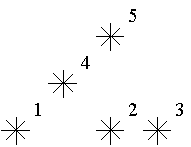
例如,上图中星星 是 级的( 在它左下),星星 是 级的。
例图中有 个 级, 个 级, 个 级, 个 级的星星。
给定星星的位置,输出各级星星的数目。
换句话说,给定 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
输入格式
第一行一个整数 ,表示星星的数目;
接下来 行给出每颗星星的坐标,坐标用两个整数 表示;
不会有星星重叠。星星按 坐标增序给出, 坐标相同的按 坐标增序给出。
输出格式
行,每行一个整数,分别是 级, 级, 级,……, 级的星星的数目。
数据范围
,
输入样例:
5
1 1
5 1
7 1
3 3
5 5
输出样例:
1
2
1
1
0
解题
方法一:树状数组
思路
题目说星星按 坐标增序给出, 坐标相同的按 坐标增序给出,那么按顺序输入每个点时:
- 在其左下角的点一定会在其之前被给出。
- 但是在其之前被给出的点不一定全是在其左下角的点。

如图所示,对于当前输入到的绿点,所有在其左下角的点(绿色区域)在之前就被输入了,而在其之前被输入但又不在其左下角的点都是那些 坐标大于当前点 坐标的点。
那么其实我们只需要维护横坐标为 的点的数量,在每次输入一个点 时先查询 横坐标上点的数量的总和就是当前星星的等级,然后再把横坐标为 的点自增 。
本题数据是时间限制是 ,所以普通的前缀和时间复杂度 肯定是过不了的,但是选择树状数组或是线段树,时间复杂度可以降到 ,这题就能过了。
注意:
- 本题中横坐标有可能为 ,而一般我们维护的线段树或树状数组都是从 开始的,所以输入坐标后最好把横坐标加 再进行操作。
- 本题要求的是每一级星星的数量,而不是每一个星星是几级,这点要注意。
代码
import java.util.*;
import java.io.*;
public class Main {
static final int N = 32010;
static int[] tr = new int[N];
static void add(int i, int x) {
for (; i <= N; i += i & -i) tr[i] += x;
}
static int query(int i) {
int sum = 0;
for (; i > 0; i -= i & -i) sum += tr[i];
return sum;
}
public static void main(String[] args) throws IOException {
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
in.nextToken();
int n = (int) in.nval;
int[] cnts = new int[n];
for (int i = 0; i < n; ++i) {
in.nextToken();
int x = (int) in.nval;
in.nextToken();
int y = (int) in.nval;
++cnts[query(x + 1)];
add(x + 1, 1);
}
for (int i = 0; i < n; ++i) System.out.println(cnts[i]);
}
}
方法二:线段树
思路
思路与前面一样,只不过单点修改和区间查询的操作改为线段树实现。
代码
import java.util.*;
import java.io.*;
public class Main {
static int N = 32010;
static class Node {
int l, r, sum;
public Node(int l, int r, int sum) {
this.l = l;
this.r = r;
this.sum = sum;
}
}
static Node[] tr = new Node[N * 4];
static void pushup(int u) {
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
static void build(int u, int l, int r) {
if (l == r) tr[u] = new Node(l, r, 0);
else {
tr[u] = new Node(l, r, 0);
int m = l + r >> 1;
build(u << 1, l, m);
build(u << 1 | 1, m + 1, r);
pushup(u);
}
}
static int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
int m = tr[u].l + tr[u].r >> 1;
int sum = 0;
if (l <= m) sum += query(u << 1, l, r);
if (r >= m + 1) sum += query(u << 1 | 1, l, r);
return sum;
}
static void add(int u, int i) {
if (tr[u].l == tr[u].r) ++tr[u].sum;
else {
int m = tr[u].l + tr[u].r >> 1;
if (i <= m) add(u << 1, i);
else add(u << 1 | 1, i);
pushup(u);
}
}
public static void main(String[] args) throws IOException {
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
in.nextToken();
int n = (int) in.nval;
int[] cnts = new int[n];
build(1, 1, N);
for (int i = 0; i < n; ++i) {
in.nextToken();
int x = (int) in.nval + 1;
in.nextToken();
int y = (int) in.nval;
++cnts[query(1, 1, x)];
add(1, x);
}
for (int x : cnts) System.out.println(x);
}
}

评论区