【算法竞赛】2023 睿抗机器人开发者大赛CAIP-编程技能赛-高职组（国赛）

RC-v1 另类单位圆

对于二维平面上的一个点，记其坐标为 $(x, y)$ 。通常当我们说到“单位圆”的时候，默认是指到原点 $(0,0)$ 的欧氏距离（即 $\sqrt{x^2 + y^2}$ ）为 $1$ 的所有点构成的曲线。现在考虑“距离”的另一种定义，令 $(x,y)$ 到原点 $(0,0)$ 的另类距离为 $|x^2−xy−y^2|$ ，则在这个另类距离下的单位圆就在二维平面上形成了另外形状的曲线。

本题给定一个正整数区间 $[a,b]$ ，求正整数坐标 $(x, y) \in [a, b] \times [a, b]$ 范围内，另类单位圆上到原点 $(0,0)$ 的欧氏距离最小和最大的点坐标。

输入格式:

输入在一行中给出闭区间的两个端点，即正整数 $a$ 和 $b$ （ $1 \le a \le b \le 10^4$ ）。

输出格式:

第一行输出到原点 $(0,0)$ 的欧氏距离最小的点坐标，第二行输出到原点 $(0,0)$ 的欧氏距离最大的点坐标。格式均为 (x, y)。

题目保证解存在且唯一。

输入样例:

10 1000

输出样例:

(21, 13)
(987, 610)

解题：枚举

本题题目读着比较绕，但其实就是让你在满足 $x, y \in [1, 1000]$ 且 $|x^2−xy−y^2| = 1$ 的所有整点 $(x, y)$ 中，分别找到 $\sqrt{x^2 + y^2}$ 最大、最小的两个点。

所以枚举 $x = 1 \dots 1000, y = 1 \dots 1000$ 当满足条件 $|x^2−xy−y^2| = 1$ 时更新最大最小点即可。

代码

以下代码为比赛过程中所写，可能比较杂乱，请见谅。

#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;

int a, b;
double mn = 1e9, mx = -1;
int mn_x, mn_y, mx_x, mx_y;

double get_d1(int x, int y) {
    return sqrt(x * x + y * y);
}

int get_d2(int x, int y) {
    return abs(x * x - x * y - y * y);
}

int main() {
    scanf("%d%d", &a, &b);
    for (int x = a; x <= b; ++x) {
        for (int y = a; y <= b; ++y) {
            if (get_d2(x, y) != 1) continue;
            int d = get_d1(x, y);
            if (d < mn) {
                mn = d;
                mn_x = x;
                mn_y = y;
            }
            if (d > mx) {
                mx = d;
                mx_x = x;
                mx_y = y;
            }
        }
    }
    printf("(%d, %d)\n", mn_x, mn_y);
    printf("(%d, %d)\n", mx_x, mx_y);

    return 0;
}

RC-v2 含茶量

ChatGPT（全名：Chat Generative Pre-trained Transformer）近期成为网络讨论的热点话题之一。本题就请你根据某社交网络中发帖的情况，统计每个人帖子中含有 ChatGPT（不区分大小写）的数量（简称“含茶量”），找出最热衷于讨论这个话题的人，即含茶量排前三的人。

输入格式:

输入在第一行中给出正整数：N（ $\le 10 ^4$ ），为参加统计的帖子数量。
随后给出 $N$ 条帖子的信息，每条格式为：第一行给出发帖人 ID，是一个长度不超过 10 位的非空数字串；第二行给出非空的帖子的内容，由不超过 140 个英文字母、数字、空格、标点（只包括 ?、, 和 .）组成，以回车结束（回车不算在 140 字内）。

输出格式:

分三行输出含茶量最高的前三个 ID，及其含茶量。有并列时按 ID 的字典序递增输出；如果有含茶量的 ID 不到三个，那么有几个就输出几个，但含茶量为 0 的不要输出。数字间以 1 个空格分隔，行首尾不得有多余空格。
题目保证至少有一个输出。

输入样例：

5
1010
I am not interested in ChatGPT.
233
I am gonna talk about chatgpt, and Chatgpt, and CHATGPT
233
they are all ChatGPT
2
I am gonna talk about chatgpt, and Chatgpt, and CHATGPT
0002
chatgp, hatGPT and Chatppt, are they all ChatGPTs?

输出样例：

233 4
2 3
0002 1

注意： 2 和 0002 是两个不同的 ID。

解题：模拟

这题是基础的字符串处理，按照题目把字符串输入，变小写，查找 "chatgpt" 出现的次数即可。

代码

以下代码为比赛过程中所写，可能比较杂乱，请见谅。

#include <cstdio>
#include <iostream>
#include <unordered_map>
#include <limits>
#include <vector>
#include <algorithm>

#define fi first
#define se second

using namespace std;

typedef pair<string, int> PSI;

int _ = []() {
    ios::sync_with_stdio(false);
    cin.tie(NULL), cout.tie(NULL);
    return 0;
}();

int n;
unordered_map<string, int> mp;

int main() {
    cin >> n;
    string id, s;
    while (n--) {
        cin >> id;
        cin.ignore(numeric_limits<streamsize>::max(), '\n');
        getline(cin, s);
        int len = s.size();
        for (int i = 0; i < len; ++i) s[i] = tolower(s[i]);
        int idx = 0, cnt = 0;
        while (idx < len) {
            int pos = s.find("chatgpt", idx);
            if (pos == s.npos) break;
            idx = pos + 7;
            ++cnt;
        }
        mp[id] += cnt;
    }
    vector<PSI> vec;
    for (PSI pr : mp) vec.push_back(pr);
    sort(vec.begin(), vec.end(), [](const PSI& a, const PSI& b) {
        if (a.se != b.se) return a.se > b.se;
        return a.fi < b.fi;
    });
    for (int i = 0; i < 3; ++i) {
        if (i == vec.size()) break;
        PSI pr = vec[i];
        if (pr.se == 0) break;
        cout << pr.fi << " " << pr.se << '\n';
    }

    return 0;
}

RC-v3 软件窗体的层级管理

在应用软件的界面中有很多选项，有些选项点开后会出现弹出窗体，而弹出的窗体界面上又有一些选项，点开后还会出现弹出窗体…… 这里我们简单假设，任何一个窗体都仅由唯一的一个选项按钮激发，并且不存在自己激发自己的窗体。
本题就请你帮助完成一个统计任务，对任一给定的按钮，给出从这个按钮出发，可以弹出最多窗体的界面是哪一层，一共能弹出多少个窗体？我们称给定按钮所在的窗体为第 1 层，同一层窗体中所有选项激发的窗体都属于下一层。
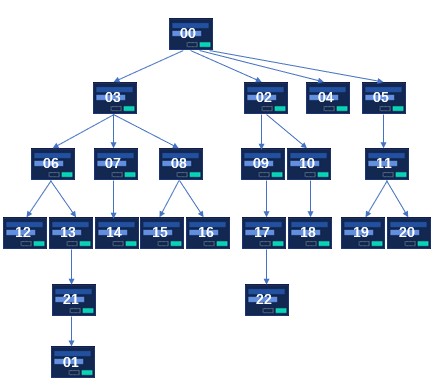
设应用软件一共设计有 N（ $<100$ ）个窗体，每个窗体有一个两位数的代号，从 00 编号到 N−1。初始界面窗体的代号为 00 。样例给出了一个有 23 个窗体的应用软件组织结构图，如下图所示。如果指定初始界面（即 00）为第 1 层的话，可以弹出最多窗体的界面是第 4 层，共有 9 个窗体；如果指定 06 号窗体为第 1 层，则相对于 06 的下面第 2 层窗体最多，有 2 个。
当有若干层弹出最多窗体数量相同时，你只需要找到最高的那个最多窗体层级即可。例如指定 09 为第 1 层时，其下方第 2、3 层都只弹出 1 个窗口，于是第 1、2、3 层的窗体数量是相同的，这时应该返回最高的第 1 层作为答案。

输入格式:

输入在第一行中给出 2 个整数：N（ $0<N<100$ ）为应用软件窗体总数，M（ $0\le M<N$ * ）为有弹出窗体选项的窗体的数量。随后 $M$ 行，每行给出一个窗体的选项信息，格式为：

ID K ID[1] ID[2] ... ID[K]

其中 ID 是该窗体的代号，K ( $>0$ ) 是弹出窗体选项数，后面给出选项对应的窗体的代号。
接下来是一个正整数 T（ $\le10$ ），最后一行给出 T 个被查询的窗体的代号。
同一行中所有数字都以空格分隔。

输出格式:

在一行中输出该运动员完成全部比赛的平均速度，单位：公里/小时。输出小数点后 1 位。

输入样例:

23 13
21 1 01
00 4 03 02 04 05
03 3 06 07 08
06 2 12 13
13 1 21
08 2 15 16
02 2 09 10
11 2 19 20
17 1 22
05 1 11
07 1 14
09 1 17
10 1 18
4
00 06 09 20

输出样例:

解题：BFS

建树，然后做 BFS 。

代码

以下代码为比赛过程中所写，可能比较杂乱，请见谅。

#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int N = 110, M = N * N;
int n, m, t;
int h[N], e[M], ne[M], idx;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs(int u) {
    queue<int> que;
    que.push(u);
    int dep = 1;
    int mx = 1, mx_dep = 1;
    while (!que.empty()) {
        int sz = que.size();
        if (sz > mx) {
            mx = sz;
            mx_dep = dep;
        }
        while (sz--) {
            u = que.front(); que.pop();
            for (int i = h[u]; ~i; i = ne[i]) {
                int v = e[i];
                que.push(v);
            }
        }
        ++dep;
    }
    printf("%d %d\n", mx_dep, mx);
}

int main() {
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof(h));
    while (m--) {
        int u, k;
        scanf("%d%d", &u, &k);
        while (k--) {
            int v; scanf("%d", &v);
            add(u, v);
        }
    }
    scanf("%d", &t);
    while (t--) {
        int x; scanf("%d", &x);
        bfs(x);
    }

    return 0;
}

RC-v4 加号放哪里

给定任一个正整数 $N$ ，我们要从它开始，经过一系列操作得到一个个位数。操作方法是在 $N$ 的各位数字之间放置一个加号，然后执行这个加法计算，得到一个新的数字 $N_1$ ，再对 $N_1$ 执行同样操作，得到 $N_2$ …… 以此类推，直到最后得到的数字只有 1 位，则停止。
例如我们从 $N=1234567890$ 出发，在 5 和 6 之间放置加号，计算 $12345+67890=80235$ ；然后在 0 和 2 之间放置加号，计算 $80+235=315$ ；然后在 1 和 5 之间放置加号，计算 $31+5=36$ ；最后在 3 和 6 之间放置加号，得到 $3+6=9$ 而停止。这样我们通过 4 次计算得到了一个个位数 9。
本题就请你为任一给定的正整数计算：最少需要多少次加号放置可以得到个位数？
注意：加号必须放置在两个数字之间，不可放置在数字的首尾。

输入格式:

输入在一行中给出一个正整数 n（ $\le10^{20}$ ）。

输出格式:

在一行中首先输出将输入的整数变为个位数，需要放置加号的最少次数；随后输出最后得到的那个个位数。如果最后得到的个位数不唯一，输出最小的那个。
数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例:

1234567890

输出样例:

3 9

样例解释：

最优划分是：

12345678+90=12345768
1234+5768=7002
7+002=9

解题：DFS

这题是个 DFS，但数据范围比较大（ $10^{20}$ > long long 类型可存储的数据范围( $\approx 10^{18}$ ) ），所以可能要用上高精度加法。

代码

以下代码为比赛过程中所写，可能比较杂乱，请见谅。

#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

int _ = []() {
    ios::sync_with_stdio(false);
    cin.tie(NULL), cout.tie(NULL);
    return 0;
}();

int mn = 1e9, mn_num = 10;

string del_pre(string x) {
    int i = 0;
    while (x[i] == '0') ++i;
    return x.substr(i);
}

string ssum(string a, string b) {
    string ans = "";
    int rem = 0;
    a = del_pre(a), b = del_pre(b);
    int n = a.size(), m = b.size();
    int i = n - 1, j = m - 1;
    for (; i >= 0 && j >= 0; --i, --j) {
        int d1 = a[i] - '0', d2 = b[j] - '0';
        int sum = d1 + d2 + rem;
        rem = sum / 10;
        ans += sum % 10 + '0';
    }
    while (i >= 0) {
        int sum = a[i] - '0' + rem;
        rem = sum / 10;
        ans += sum % 10 + '0';
        --i;
    }
    while (j >= 0) {
        int sum = b[j] - '0' + rem;
        rem = sum / 10;
        ans += sum % 10 + '0';
        --j;
    }
    if (rem) ans += rem + '0';
    reverse(ans.begin(), ans.end());
    return del_pre(ans);
}

void dfs(string x, int cnt) {
    if (cnt > mn) return;
    int n = x.size();
    if (n == 1 && stoi(x) <= mn_num) {
        mn = cnt;
        mn_num = stoi(x);
        return;
    }
    for (int i = 1; i < n; ++i) {
        string sum = ssum(x.substr(0, i), x.substr(i));
        dfs(sum, cnt + 1);
    }
}

int main() {
    string n; cin >> n;
    dfs(n, 0);
    cout << mn << ' ' << mn_num << '\n';

    return 0;
}

目录CONTENT

【算法竞赛】2023 睿抗机器人开发者大赛CAIP-编程技能赛-高职组（国赛）

RC-v1 另类单位圆

解题：枚举

代码

RC-v2 含茶量

解题：模拟

代码

RC-v3 软件窗体的层级管理

解题：BFS

代码

RC-v4 加号放哪里

解题：DFS

代码

评论区