侧边栏壁纸
博主头像
GabrielxD

列車は必ず次の駅へ。では舞台は？私たちは？

  • 累计撰写 675 篇文章
  • 累计创建 128 个标签
  • 累计收到 22 条评论
标签搜索

目 录CONTENT

文章目录
算法

【算法竞赛】2021 RoboCom 世界机器人开发者大赛-本科组（决赛）（第二题无解题，待补充）

GabrielxD
GabrielxD
2022-08-05 / 0 评论 / 0 点赞 / 476 阅读 / 4,200 字
温馨提示：
本文最后更新于 2022-08-05，若内容或图片失效，请留言反馈。部分素材来自网络，若不小心影响到您的利益，请联系我们删除。

7-1 绿地围栏

wl.png

市政规划了一块绿地，需要采购一批围栏将绿地围起来。

为了简单起见，我们假设绿地的形状是个封闭连通的规则多边形，即所有边都是互相垂直或平行的，并且没有交叉的十字边。我们指定某条垂直边上的一个点为原点 (0,0)，然后按照顺时针记录这个多边形的拐角顶点的位置。显然两个相邻的点坐标中，总有一个是不变的，因为当我们从一个点沿着平行于 x 轴的边移动到下一个点时，这两个点的 y 坐标是不变的；当我们从一个点沿着平行于 y 轴的边移动到下一个点时，这两个点的 x 坐标是不变的，所以我们可以用一种简化的方式去记录这些拐角，即对于从原点开始顺时针出现的拐角点 P1、P2、P3、…… 我们只需要记录 y1、x2、y3、…… 即可，其中 Pi 的坐标是 (xi,yi)。

采购的围栏每一条有固定长度 L，但是可以从任何地方弯折 90 度角，并且超长的部分也可以截掉。我们需要在两条围栏的衔接处打桩固定连接。现按顺时针方向给出绿地多边形各个拐角的简化坐标列表，请你计算需要采购多少条围栏，以及应该在哪里打桩。

输入格式：

输入第一行给出 2 个正整数，分别是：N（≤103），为绿地拐角点的个数（原点不算在内）；以及 L（≤100），是一条围栏的长度。

随后给出 N 个整数，即从原点开始，按顺时针方向给出多边形各个拐角的简化坐标列表。每个坐标的绝对值均不超过 104。数字间以空格分隔。题目保证没有重叠或交叉的边。

输出格式：

每行按格式 x y 输出一对坐标，即从原点出发顺时针给出的打桩点的坐标 (x,y)。注意原点肯定要打一个桩。规定从原点出发顺时针布置围栏，优先使用整条围栏，最后回到原点时，有多余的围栏才会被截掉。

输入样例：

14 5
2 1 1 4 3 5 2 6 -1 4 0 2 -1 0

输出样例：

0 0
2 1
5 3
6 -1
2 0

样例说明：

样例对应的多边形如下图所示（其中红色方块为原点）：

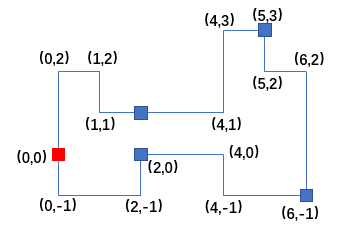
sample.png

容易算出围栏的总长度为 24，而每条围栏的长度为 5，所以需要 5 条围栏，多余的 1 个单位长度的围栏可以拆掉。从红色的原点出发，每隔 5 个单位打一根桩，图中蓝色方块即为打桩的位置。

解题：模拟

思路

按题目给出的规则输入并存储所有拐点坐标，由于围栏是首尾相接且输入没给出第一个点 (0,0)(0, 0)，所以要把点 (0,0)(0, 0) 加入坐标数组的尾部。然后就可以开始模拟：

维护已走过距离(len)、当前坐标(x, y)，根据拐点的路径每次前进一个单位长度(距离自增)，当距离等于 L 时就输出一次当前坐标，并把距离置零。

代码
#include <iostream>

using namespace std;

int main() {
    int N, L;
    scanf("%d%d", &N, &L);
    int points[N + 1][2];
    points[N][0] = points[N][1] = 0;
    int point[2] = {0, 0};
    for (int i = 0; i < N; ++i) {
        scanf("%d", &point[!(i & 1)]);
        points[i][0] = point[0];
        points[i][1] = point[1];
    }
    printf("0 0\n");
    int x = 0, y = 0, nx = points[0][0], ny = points[0][1], len = 0;
    for (int i = 0; i <= N;) {
        if (len == L) {
            if (x == 0 && y == 0) break;
            printf("%d %d\n", x, y);
            len = 0;
        }
        if (x == nx && y == ny) {
            ++i;
            nx = points[i][0], ny = points[i][1];
            continue;
        }
        ++len;
        if (x == nx) {
            if (y < ny) ++y; else --y;
        } else {
            if (x < nx) ++x; else --x;
        }
    }

    return 0;
}

7-2 队列插入

现在有一个空队列 Q 以及 N 个数字需要按顺序插入，你可以选择插入队列的头部或尾部，请问在合理选择插入方式的前提下，插入后的队列的最长上升子序列的长度最大是多少？

最长上升子序列指的是在一个给定的数值序列中，找到一个子序列，使得这个子序列元素的数值依次递增，并且这个子序列的长度尽可能地大。子序列指的是通过删除原序列中零个或多个元素后获得的序列。

输入格式:

输入第一行是一个数 N (1≤N≤1000)，表示有 N 个要按顺序插入的数字。

接下来一行 N 个数，表示要插入的数字，数字已经按插入顺序排列好，并且都在 32 位整数范围内。

输出格式:

输出两行，第一行是一个数字，表示最大的最长上升子序列的长度。

接下来一行，输出插入的方案，其中用L表示插入到头部，用R表示插入到尾部。当有多个相同长度的方案时，选择字典序最小的方案（L 的字典序小于 R）。

输入样例:

8
1 3 2 4 2 4 5 0

输出样例:

5
LLLLLRRL

样例解释：

样例最后队列内容为：0 2 4 2 3 1 4 5

解题：待补充

7-3 账户安全预警

拼题 A 系统为提高用户账户的安全性，打算开发一个自动安全预警的功能。对每个账户的每次登录，系统会记录其登录的 IP 地址。每隔一段时间，系统将统计每个账户从多少不同的 IP 地址分别登录了多少次。如果某个账户的登录 IP 超过了 TIP 种，并且登录过于频繁，超过了 Tlogin 次，则会自动向管理员发出警报。

下面就请你实现这个预警功能。

输入格式：

输入首先在第一行中给出三个正整数：N（≤104）为登录记录的条数；TIP 和
*Tlogin*​，定义如题面中所描述，均不超过 100。

随后 N 行，每行格式为：

账户邮箱 IP地址

其中 账户邮箱 为长度不超过 40 的、不包含空格的非空字符串；IP地址 为形如 xxx.xxx.xxx.xxx 的合法 IP 地址。

输出格式：

按照登录所用不同 IP 的数量的非递增顺序，输出每个预警账户的信息。格式为：

账户邮箱
IP1 登录次数
IP2 登录次数
……

其中 IP 按登录次数的非递增顺序输出，如有并列，则按 IP 的递增字典序输出。此外，对所用不同 IP 的数量并列的用户，按其账户邮箱的递增字典序输出。

另一方面，即使没有账户达到预警线，也输出登录所用不同 IP 的数量最多的一批账户的信息。

输入样例 1：

24 3 4
daohaole@qq.com 218.109.231.189
1jiadelaolao@163.com 112.192.203.187
chenyuelaolao@zju.edu.cn 112.18.235.143
jiadelaolao@163.com 112.192.203.187
chenyuelaolao@zju.edu.cn 113.18.235.143
jiadelaolao@163.com 111.192.203.187
daohaole@qq.com 218.109.231.189
chenyuelaolao@zju.edu.cn 111.18.235.143
1jiadelaolao@163.com 115.192.203.187
daohaole@qq.com 113.189.58.141
1jiadelaolao@163.com 111.192.203.187
daohaole@qq.com 112.18.58.145
1jiadelaolao@163.com 114.192.203.187
chenyuelaolao@zju.edu.cn 112.18.235.143
daohaole@qq.com 123.89.158.214
chenyuelaolao@zju.edu.cn 112.18.235.143
youdaohaole@qq.com 218.109.231.189
jiadelaolao@163.com 113.192.203.187
youdaohaole@qq.com 218.109.231.189
jiadelaolao@163.com 114.192.203.187
youdaohaole@qq.com 113.189.58.141
youdaohaole@qq.com 123.89.158.214
1jiadelaolao@163.com 113.192.203.187
youdaohaole@qq.com 112.18.58.145

输出样例 1：

1jiadelaolao@163.com
111.192.203.187 1
112.192.203.187 1
113.192.203.187 1
114.192.203.187 1
115.192.203.187 1
daohaole@qq.com
218.109.231.189 2
112.18.58.145 1
113.189.58.141 1
123.89.158.214 1
youdaohaole@qq.com
218.109.231.189 2
112.18.58.145 1
113.189.58.141 1
123.89.158.214 1

输入样例 2：

24 5 8
daohaole@qq.com 218.109.231.189
1jiadelaolao@163.com 112.192.203.187
chenyuelaolao@zju.edu.cn 112.18.235.143
jiadelaolao@163.com 112.192.203.187
chenyuelaolao@zju.edu.cn 113.18.235.143
jiadelaolao@163.com 111.192.203.187
daohaole@qq.com 218.109.231.189
chenyuelaolao@zju.edu.cn 111.18.235.143
1jiadelaolao@163.com 115.192.203.187
daohaole@qq.com 113.189.58.141
1jiadelaolao@163.com 111.192.203.187
daohaole@qq.com 112.18.58.145
1jiadelaolao@163.com 114.192.203.187
chenyuelaolao@zju.edu.cn 112.18.235.143
daohaole@qq.com 123.89.158.214
chenyuelaolao@zju.edu.cn 112.18.235.143
youdaohaole@qq.com 218.109.231.189
jiadelaolao@163.com 113.192.203.187
youdaohaole@qq.com 218.109.231.189
jiadelaolao@163.com 114.192.203.187
youdaohaole@qq.com 113.189.58.141
youdaohaole@qq.com 123.89.158.214
1jiadelaolao@163.com 113.192.203.187
youdaohaole@qq.com 112.18.58.145

输出样例 2：

1jiadelaolao@163.com
111.192.203.187 1
112.192.203.187 1
113.192.203.187 1
114.192.203.187 1
115.192.203.187 1

解题：哈希表 排序

思路

输入所有数据到哈希表然后按题目要求排序输出即可。

注意：账户排序时用规则是不同 IP 的数量(Account.ips.size())而不是账户的总登录次数(Account.login)，避免多次调用 size() 函数取长度影响效率可以直接维护一个变量。账户总登录次数只在区分预警账户的时候用到了。

代码
#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>

using namespace std;

int _ = []() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    return 0;
}();

struct IP {
    string ip_str;
    int login;

    friend bool operator<(const IP& a, const IP& b) {
        return a.login == b.login ? a.ip_str < b.ip_str : a.login > b.login;
    }
};

struct Account {
    string email;
    vector<IP> ips;
    int login, ip_cnt;

    Account(const string& email, const vector<IP>& ips, int login) :
            email(email), ips(ips), login(login), ip_cnt(ips.size()) { }

    friend bool operator<(const Account& a, const Account& b) {
        return a.ip_cnt == b.ip_cnt ? a.email < b.email : a.ip_cnt > b.ip_cnt;
    }
};

int main() {
    int N, T_IP, T_login;
    cin >> N >> T_IP >> T_login;
    string email, ip_str;
    unordered_map<string, unordered_map<string, int>> mp;
    while (N--) {
        cin >> email >> ip_str;
        ++mp[email][ip_str];
    }
    vector<Account> accs, anss;
    for (auto& pr : mp) {
        int cnt = 0;
        vector<IP> ips;
        for (auto& v : pr.second) {
            cnt += v.second;
            ips.push_back({v.first, v.second});
        }
        sort(ips.begin(), ips.end());
        Account acc = {pr.first, ips, cnt};
        accs.push_back(acc);
        if (ips.size() > T_IP && cnt > T_login) anss.push_back(acc);
    }
    if (anss.size()) {
        sort(anss.begin(), anss.end());
        for (auto& acc : anss) {
            cout << acc.email << "\n";
            for (IP& ip : acc.ips) {
                cout << ip.ip_str << " " << ip.login << "\n";
            }
        }
    } else {
        sort(accs.begin(), accs.end());
        int max_ip_cnt = accs[0].ip_cnt;
        for (auto it = accs.begin(); it != accs.end() && it->ip_cnt == max_ip_cnt; ++it) {
            cout << it->email << "\n";
            for (IP& ip : it->ips) {
                cout << ip.ip_str << " " << ip.login << "\n";
            }
        }
    }

    return 0;
}

7-4 猛犸不上 Ban

mammoth-gd01e31f27_640.png

在一个名叫刀塔的国家里，有一只猛犸正在到处跑着，希望能够用它的长角抛物技能来撞飞别人。已知刀塔国有 N 座城市，城市之间由 M 条道路互相连接，为了拦住这头猛犸，每条道路上设置了 Vi 人的团队。

这只猛犸从 S 号城市出发，它可以选择：

  1. 在不重复地经过若干条道路后回到 S 号城市；
  2. 在不重复地经过若干条道路后到达 T 号城市。

猛犸经过一条道路后，就会把路上的人全部撞飞。作为一头爱喝雪碧的仁慈的猛犸，自然希望尽可能的少撞飞人。请你帮忙计算一下在最优的选择下，最少需要撞飞多少人才能够到达目标城市？

输入格式:

输入第一行是四个正整数 N,M,S,T (2≤N≤500,1≤M≤105)，表示有 N 个城市，M 条道路，猛犸从 S 号城市出发，可以选择到达 T 号城市。

接下来的 M 行，每行三个正整数 Xi,Yi,Vi (0≤*Vi*≤100)，表示从 Xi 号城市到 Yi 号城市有一条道路，道路上有 Vi 人的团队。道路可双向通行，城市编号从 1 开始，两个城市之间最多只有一条道路，且没有一条道路连接相同的城市。

数据保证两种选择里至少有一种是可行的。

输出格式:

输出两行，第一行是两个数字，分别对应上面的两种选择分别最少需要撞飞多少人。如果无论撞飞多少人都无法满足选择要求，则输出 -1。

第二行是一个句子，如果第一种（回到原点）的选择比较好，就输出 Win!，否则输出Lose!。

输入样例:

5 6 1 5
1 2 1
2 3 2
3 4 3
4 1 5
3 5 4
4 5 1

输出样例:

在这里给出相应的输出。例如：

11 6
Lose!

解题：Dijkstra 算法

思路

其实就是求 T->S 的最短路和 S->S 的最短路。T->S 的最短路比较好求，直接跑一遍朴素 Dijkstra 算法(dijkstra1())就行了。S->S的最短路需要拆解问题：

S->S 的最短路可以看作是 S->X 的最短路加上 X->S 的最短路，然后注意有限定条件不重复边。具体做法是：先对 S 跑一遍 Dijkstra 算法求出所有点到点 S 的最短路(可以直接用上面求 T->S 的结果)，期间记录路径(path)这样就可以知道 S->X 的最短路途中经过了哪些点。然后枚举除了 S 以外 S 可以到达的所有点当作途径点 X，那么就可以在 path 中这个路径转换成一个禁止数组(forbid)标注这些边已经用过了不能再用，再然后对于这个点 X 跑一遍 Dijkstra 算法(dijkstra2())到 S，期间遇到 forbid 标记的边就跳过。那么所有可能的两条最短路相加中的最小值(min(ans_S, dist[i] + dist2[i]))就是 S->S 的最短路。

最后根据题目要求输出。

代码
 #include <iostream>

using namespace std;

const int MAX_N = 501, INF = 0x3f3f3f3f;
int N, M, S, T;
int graph[MAX_N][MAX_N], dist[MAX_N], dist2[MAX_N], path[MAX_N];
bool visited[MAX_N], forbid[MAX_N][MAX_N];

int dijkstra1() {
    for (int i = 1; i <= N; ++i) {
        dist[i] = INF;
        path[i] = -1;
    }
    dist[S] = 0;
    for (int i = 1; i <= N; ++i) {
        int mn = -1;
        for (int j = 1; j <= N; ++j) {
            if (!visited[j] && (mn == -1 || dist[j] < dist[mn]))mn = j;
        }
        visited[mn] = true;
        for (int j = 1; j <= N; ++j) {
            if (dist[j] > dist[mn] + graph[mn][j]) {
                dist[j] = dist[mn] + graph[mn][j];
                path[j] = mn;
            }
        }
    }
    return dist[T];
}

void dijkstra2(int ori) {
    for (int i = 1; i <= N; ++i) {
        dist2[i] = INF;
        visited[i] = false;
    }
    dist2[S] = 0;
    for (int i = 1; i <= N; ++i) {
        int mn = -1;
        for (int j = 1; j <= N; ++j) {
            if (!visited[j] && (mn == -1 || dist2[j] < dist2[mn]))mn = j;
        }
        if (mn == ori) break;
        visited[mn] = true;
        for (int j = 1; j <= N; ++j) {
            if (forbid[j][mn]) continue;
            dist2[j] = min(dist2[j], dist2[mn] + graph[mn][j]);
        }
    }
}

int main() {
    scanf("%d%d%d%d", &N, &M, &S, &T);
    for (int i = 1; i <= N; ++i) {
        for (int j = 1; j <= N; ++j) {
            graph[i][j] = graph[j][i] = INF;
        }
    }
    while (M--) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        graph[u][v] = graph[v][u] = w;
    }
    int ans_T = dijkstra1(), ans_S = INF;
    for (int i = 1; i <= N; i++) {
        if (i == S) continue;
        for (int x = path[i], y = i; x != -1; y = path[y], x = path[x])
            forbid[x][y] = forbid[y][x] = true;
        dijkstra2(i);
        ans_S = min(ans_S, dist[i] + dist2[i]);
        for (int x = path[i], y = i; x != -1; y = path[y], x = path[x])
            forbid[x][y] = forbid[y][x] = false;
    }
    printf("%d %d\n", ans_S == INF ? -1 : ans_S, ans_T == INF ? -1 : ans_T);
    printf(ans_S < ans_T ? "Win!" : "Lose!");

    return 0;
}
0
图(数据结构) 排序 模拟 哈希表 单源最短路径 Dijkstra算法 RoboCom
版权归属： GabrielxD
本文链接： https://gabrielxd.com/archives/algorithm-robocom2021-caip-group-a-final-contest
许可协议： 本文使用《署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0)》协议授权

评论区