【单源最短路】Car的旅行路线

题目

P1027 [NOIP2001 提高组] Car 的旅行路线

题目描述

又到暑假了，住在城市 A 的 Car 想和朋友一起去城市旅游。
她知道每个城市都有 $4$ 个飞机场，分别位于一个矩形的 $4$ 个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第 $i$ 个城市中高速铁路了的单位里程价格为 $T_i$ ，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为 $t$ 。

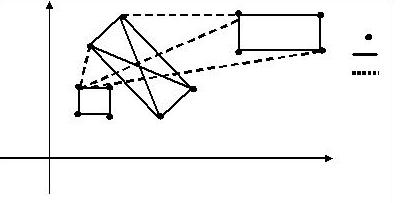
图例（从上而下）

机场
高速铁路
飞机航线

注意：图中并没有标出所有的铁路与航线。

那么 Car 应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市 A 到 B 的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入格式

第一行为一个正整数 $n$ ，表示有 $n$ 组测试数据。

每组的第一行有 $4$ 个正整数 $s,t,A,B$ 。

$S$ 表示城市的个数， $t$ 表示飞机单位里程的价格， $A$ ， $B$ 分别为城市A，B 的序号。

接下来有 $S$ 行，其中第 $i$ 行均有 $7$ 个正整数 $x_{i1},y_{i1},x_{i2},y_{i2},x_{i3},y_{i3},T_i$ ，这当中的 ( $x_{i1},y_{i1}$ )，( $x_{i2},y_{i2}$ )，( $x_{i3},y_{i3}$ )分别是第 $i$ 个城市中任意 $3$ 个机场的坐标， $T_i$ 为第 $i$ 个城市高速铁路单位里程的价格。

输出格式

共有 $n$ 行，每行 $1$ 个数据对应测试数据。
保留一位小数。

样例 #1

样例输入 #1

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

样例输出 #1

47.5

提示

【数据范围】

对于 $100\%$ 的数据， $1\le n \le 10$ ， $1\le S \le 100$ ， $1\le A,B \le S$

【题目来源】

NOIP 2001 提高组第四题

解题

方法一：SPFA算法

思路

本题是单纯的单源最短路问题，但是建图比较麻烦：

先利用已有的三个点的坐标，根据勾股定理的逆定理，判断出直角边：

例如上图中若有 $AB^2 + BC^2 = AC^2$ 则说明 $AB, BC$ 为直角边。

然后根据矩形对边平行的性质仿照 $B \to A$ 移动 $C \to D$ 就能得到 $D$ 点的坐标：

因为“任意两个不同城市的机场之间均有航线”、“同一个城市中两个机场之间有一条笔直的高速铁路”，那么每一个顶点都可以与其它所有顶点连一条无向边，也就是说这是一个完全图，但题目给出的数据范围最多有 $S=100$ 个城市，那么最多会连 $2 \times 4S(4S-1) = 319200$ 条边，所以用邻接矩阵或者邻接表存图都可以。

注意算边权的时候，如果两点在同一城市，就要用距离乘以该城市的高速铁路价格 $T_i$ ，否则，走的是飞行航线，需乘以航线单价 $t$ 。

代码

不存图，边做SPFA边算边权：

import java.util.*;
import java.io.*;

public class Main {
    static final int INF = 0x3f3f3f3f;
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    static int n, T, A, B;
    static int[][] pts;
    static int[] ts;

    static int getSquDist(int x1, int y1, int x2, int y2) {
        int dx = x1 - x2, dy = y1 - y2;
        return dx * dx + dy * dy;
    }

    static double getDist(int x1, int y1, int x2, int y2) {
        return Math.sqrt(getSquDist(x1, y1, x2, y2));
    }

    static int[] getD(int ax, int ay, int bx, int by, int cx, int cy) {
        int squAB = getSquDist(ax, ay, bx, by);
        int squBC = getSquDist(bx, by, cx, cy);
        int squAC = getSquDist(ax, ay, cx, cy);
        if (squAB + squBC == squAC) return new int[]{cx + ax - bx, cy + ay - by, 0};
        else if (squAB + squAC == squBC) return new int[]{ax + bx - ax, cy + by - ay, 0};
        else if (squBC + squAC == squAB) return new int[]{ax + bx - cx, ay + by - cy, 0};
        return null;
    }

    static double spfa(int src, int dest) {
        double[] dists = new double[n * 4 + 1];
        Arrays.fill(dists, INF);
        Queue<Integer> que = new LinkedList<>();
        boolean[] has = new boolean[n * 4 + 1];
        int st = (src - 1) * 4 + 1, ed = st + 4;
        for (int i = st; i < ed; ++i) {
            dists[i] = 0.0;
            que.offer(i);
            has[i] = true;
        }
        while (!que.isEmpty()) {
            int u = que.poll();
            has[u] = false;
            int x = pts[u][0], y = pts[u][1];
            for (int v = 1; v <= n * 4; ++v) {
                if (v == u) continue;
                double d = getDist(x, y, pts[v][0], pts[v][1]);
                double w = pts[u][2] == pts[v][2] ? ts[pts[u][2]] * d : T * d;
                if (dists[u] + w < dists[v]) {
                    dists[v] = dists[u] + w;
                    if (!has[v]) {
                        que.offer(v);
                        has[v] = true;
                    }
                }
            }
        }
        double mn = INF;
        st = (dest - 1) * 4 + 1; ed = st + 4;
        for (int i = st; i < ed; ++i) mn = Math.min(mn, dists[i]);
        return mn;
    }

    static void solve() throws IOException {
        in.nextToken(); n = (int) in.nval;
        in.nextToken(); T = (int) in.nval;
        in.nextToken(); A = (int) in.nval;
        in.nextToken(); B = (int) in.nval;
        pts = new int[n * 4 + 1][3];
        ts = new int[n + 1];
        for (int i = 1; i <= n * 4; i += 4) {
            int city = i / 4 + 1;
            in.nextToken(); pts[i][0] = (int) in.nval;
            in.nextToken(); pts[i][1] = (int) in.nval;
            in.nextToken(); pts[i + 1][0] = (int) in.nval;
            in.nextToken(); pts[i + 1][1] = (int) in.nval;
            in.nextToken(); pts[i + 2][0] = (int) in.nval;
            in.nextToken(); pts[i + 2][1] = (int) in.nval;
            in.nextToken(); ts[city] = (int) in.nval;
            int[] pos = getD(pts[i][0], pts[i][1], pts[i + 1][0], pts[i + 1][1], pts[i + 2][0], pts[i + 2][1]);
            pts[i + 3] = pos;
            pts[i][2] = pts[i + 1][2] = pts[i + 2][2] = pts[i + 3][2] = city;
        }
        System.out.printf("%.1f\n", spfa(A, B));
    }

    public static void main(String[] args) throws IOException {
        in.nextToken(); int t = (int) in.nval;
        while (t-- > 0) solve();
    }
}

邻接表存图：

import java.util.*;
import java.io.*;

public class Main {
    static final int INF = 0x3f3f3f3f;
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer in = new StreamTokenizer(br);
    static int s, T, A, B;
    static int n, m;
    static int[][] pts;
    static int[] ts;
    static int[] h, e, ne;
    static double[] w;
    static int idx;

    static int getSquDist(int x1, int y1, int x2, int y2) {
        int dx = x1 - x2, dy = y1 - y2;
        return dx * dx + dy * dy;
    }

    static double getDist(int x1, int y1, int x2, int y2) {
        return Math.sqrt(getSquDist(x1, y1, x2, y2));
    }

    static void add(int a, int b, double c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }

    static int[] getD(int ax, int ay, int bx, int by, int cx, int cy) {
        int squAB = getSquDist(ax, ay, bx, by);
        int squBC = getSquDist(bx, by, cx, cy);
        int squAC = getSquDist(ax, ay, cx, cy);
        if (squAB + squBC == squAC) return new int[]{cx + ax - bx, cy + ay - by, 0};
        else if (squAB + squAC == squBC) return new int[]{ax + bx - ax, cy + by - ay, 0};
        else if (squBC + squAC == squAB) return new int[]{ax + bx - cx, ay + by - cy, 0};
        return null;
    }

    static double spfa(int src, int dest) {
        double[] dists = new double[n + 1];
        Arrays.fill(dists, INF);
        Queue<Integer> que = new LinkedList<>();
        boolean[] has = new boolean[n + 1];
        int st = (src - 1) * 4 + 1, ed = st + 4;
        for (int i = st; i < ed; ++i) {
            dists[i] = 0.0;
            que.offer(i);
            has[i] = true;
        }
        while (!que.isEmpty()) {
            int u = que.poll();
            has[u] = false;
            for (int i = h[u]; i != -1; i = ne[i]) {
                int v = e[i];
                if (dists[u] + w[i] < dists[v]) {
                    dists[v] = dists[u] + w[i];
                    if (!has[v]) {
                        que.offer(v);
                        has[v] = true;
                    }
                }
            }
        }
        double mn = INF;
        st = (dest - 1) * 4 + 1; ed = st + 4;
        for (int i = st; i < ed; ++i) mn = Math.min(mn, dists[i]);
        return mn;
    }

    static void solve() throws IOException {
        in.nextToken(); s = (int) in.nval;
        in.nextToken(); T = (int) in.nval;
        in.nextToken(); A = (int) in.nval;
        in.nextToken(); B = (int) in.nval;
        n = s * 4; m = 2 * n * n;
        pts = new int[n + 1][3];
        ts = new int[s + 1];
        h = new int[n + 1];
        Arrays.fill(h, -1);
        e = new int[m];
        ne = new int[m];
        w = new double[m];
        for (int i = 1; i <= n; i += 4) {
            int city = i / 4 + 1;
            in.nextToken(); pts[i][0] = (int) in.nval;
            in.nextToken(); pts[i][1] = (int) in.nval;
            in.nextToken(); pts[i + 1][0] = (int) in.nval;
            in.nextToken(); pts[i + 1][1] = (int) in.nval;
            in.nextToken(); pts[i + 2][0] = (int) in.nval;
            in.nextToken(); pts[i + 2][1] = (int) in.nval;
            in.nextToken(); ts[city] = (int) in.nval;
            int[] pos = getD(pts[i][0], pts[i][1], pts[i + 1][0], pts[i + 1][1], pts[i + 2][0], pts[i + 2][1]);
            pts[i + 3] = pos;
            pts[i][2] = pts[i + 1][2] = pts[i + 2][2] = pts[i + 3][2] = city;
        }
        for (int u = 1; u <= n; ++u) {
            int cu = pts[u][2];
            for (int v = 1; v <= n; ++v) {
                double d = getDist(pts[u][0], pts[u][1], pts[v][0], pts[v][1]);
                double w = d * (cu == pts[v][2] ? ts[pts[u][2]] : T);
                add(u, v, w); add(v, u, w);
            }
        }
        System.out.printf("%.1f\n", spfa(A, B));
    }

    public static void main(String[] args) throws IOException {
        in.nextToken(); int t = (int) in.nval;
        while (t-- > 0) solve();
    }
}

目录CONTENT

【单源最短路】Car的旅行路线

题目

解题

方法一：SPFA算法

思路

代码

评论区